LOS LIMITES
-Limite de un punto.
Se dice que el límite de f(x) cuando x tiende al punto a es L si la función toma valores cada vez más cercanos a L cuando x toma valores cada vez más cercanos al punto a.

-Límite en un punto infinito
Se dice que el límite de f(x) cuando x tiende a más infinito (+∞) es L si la función toma valores cada vez más cercanos a L cuando x crece indefinidamente.
Se expresa de esta manera:
EL NÚEMRO E
El número e es un número irracional, es decir, un número que no o puede expresarse como el cociente exacto de dos números enteros, cuyo número de decimales que contiene es infinito y, por tanto, estos decimales se siguen sin una secuencia lógica. Por lo tanto, se opone a un número racional cuyo desarrollo decimal es periódico, un cociente de dos números enteros cuya escritura decimal puede ser infinita, pero que en este caso es periódica.
El número e debe su nombre a sus descubridores ya que en algunas ocasiones podemos encontrar este número de la forma número de Euler (Leonhard Euler) o constante de Napier (John Napier).
Se habla de de sucesión porque se puede asignar valores ordenados a la variable n.
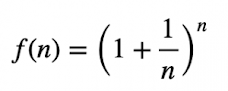
La expresión matemática generalizada de la sucesión sería teniendo en cuenta que n se aproxima a infinito. En el siguiente gráfico se puede ver como la sucesión (línea negra) va acercándose al límite (línea azul), es decir, al número e, a medida que aumenta n.



No hay comentarios:
Publicar un comentario